Self-Adjusting Lists

1. Problem: linear search

Given $n$ elements, and a key for an element, search for it by linearly iterating through the list.

Worst case: $n$ comparisons

Average case: If all elements have equal probability of search, then the expected time is $\frac{n+1}{2}$ in successful case and $n$ for an unsuccessful.

How did we get $\frac{n+1}{2}$? $$\begin{aligned} \frac{1}{n}\cdot 1 + \frac{1}{n} \cdot 2 + \frac{1}{n} \cdot 3 + \dots + \frac{1}{n} \cdot n \= \frac{1}{n}(1+2+ \dots + n) \= \frac{n+1}{2} \end{aligned}$$

2. Real Questions

1. What if the probabilities of access differ?

Let $p_{i}$ be the probability of requesting element $i$.

2. What if these (independent) probabilities are not given?

3. How do solutions compare with the best we could do

3. Self-adjusting data structures - Adapt to changing probabilities

1. If probabilities are the same and independent, it doesn't matter how you change the structure

2. If both probabilities and list are fixed, minimize $\sum_{i=1}^n i p_{i}$

Greedy: element with the highest probability should be placed first.

Let $S_{opt}$ be the starting optimal solution.

3. How can we adapt to changes in probability or self-adjust?

Move elements forward as accessed.

Heuristics:

Move-to-front (MTF): after an item is accessed, move it to the front of the list.
Transpose (TR): After an item is accessed, exchange it with the immediate preceding item.
Frequency count (FC): Maintain a frequency count for each item, initially $0$. Increase the count of an item by $1$ whenever it is accessed. Maintain a list such that the items are in decreasing order by frequency count.

2. Model

Start with an empty list. Scan for elements requested. If not present Insert (and change) as if found at the end of the list (then apply heuristic)

Cost: number of comparisons

3. The cost of MTF $\leq 2\cdot S_{opt}$ for any sequence of requests

Proof

Consider an arbitrary list, but focus on searches for $b$, $c$ (two arbitrary elements), and "unsuccessful comparisons" where we compare query value $b$ against $c$ or $c$ against $b$.

Assume the request sequence has $k$ $b$'s and $m$ $c$'s (no assumption on order of searches). Without loss of generality, assume that $k \leq m$.

$S_{opt}$ order is $c b$ and there are $k$ unsuccessful comparisons.

What order of requests maximizes this number under MTF?

Clearly, $C^{m-k}(bc)^k$.

There are $2k$ unsuccessful comparisons.

Under MTF, an unsuccessful comparison will happen whenever the request sequence changes, from $b$ to $c$ or $c$ to $b$.

Since each change involves a $b$ and each $b$ can be involved in at most two changes, the total number of such changes is $\leq 2k$.

This holds for any pair of elements, sum over all the total number of unsuccessful comparisons of MTF $$\leq 2 \cdot \dots \cdot S_{opt}$$

🔼 What is this?

We also observe that the total number of successful comparisons of MTF and the total number of successful comparisons of $S_{opt}$ are equal.

And the number of cost of MTF is at most $2 \cdot S_{opt}$.

4. This bound is tight.

Given $a_{1}, a_{2}, a_{3}, \dots , a_{n}$, we repeatedly ask for the last element in the list. So, the elements are requested equally often.

The cost of MTF is $n$ comparisons per search. But for the $S_{opt}$, every item has the same probability of being accessed, so the cost is $\frac{n+1}{2}$.

5. For some sequences, MTF does much better

Consider the following sequence of requests $$a_{1}^n \ a_{2}^n \dots a_{n}^n$$ The cost of $S_{opt}$ would be $\frac{n+1}{2}$

The cost of MTF would be $$\begin{aligned} \frac{(1+(n-1)) + (2+(n-1)) + (3+(n-1)) + \dots + (n + (n-1))}{n^2}\ = \frac{\frac{n(n+1)}{2} + n(n-1)}{n^2} \ = \frac{3}{2} - \Theta\left( \frac{1}{n} \right) \end{aligned}$$

5. Dynamic optimality

1. Online vs Offline

Online: Must respond as requests come
Offline: Get to see the entire schedule and determine how to move values

2. Competitive ratio of $Alg$

$=$ worst case of $\frac{\text{Online time of }Alg}{\text{Optimal offline time}}$

3. A method is "competitive" if this ratio is a constant

4. Model

Search for or change element in position $i$: scan to location $i$ at cost $i$
Free exchange: exchanges (swaps) between adjacent elements that are required to move element $i$ closer to the front are free of cost
Paid exchange: any other exchange (swapping) between adjacent elements costs $1$

Before cost of self-adjusting

$Access$: costs $i$ if element is in position $i$
$Delete$: costs $i$ if element is in position $i$
$Insert$: costs $n+1$ if $n$ elements are already there

5. Definitions

Request sequence: $M$ queries, $n$ max data values
Start with empty list
Cost model for a search that ends with finding the element at position $i$ is $i +$ number of paid exchanges
$C_{A}(S)$: the total cost of all operations for an algorithm $A$, not counting paid exchanges
$X_{A}(S)$: number of paid exchanges $$X_{MTF}(S) = X_{TR}(S) = X_{FC}(S) = 0$$
$F_{A}(S)$: number of free exchanges

Observation: $F_{A}(S) \leq C_{A}(S) - M$ After accessing the $i$th element, there are $\leq i - 1$ free exchanges.

Claim: $C_{MTF} \leq 2 C_{A}(S) + X_{A}(S) - F_{A}(S) - M$ for any algorithm $A$ starting with an empty set

Proof:

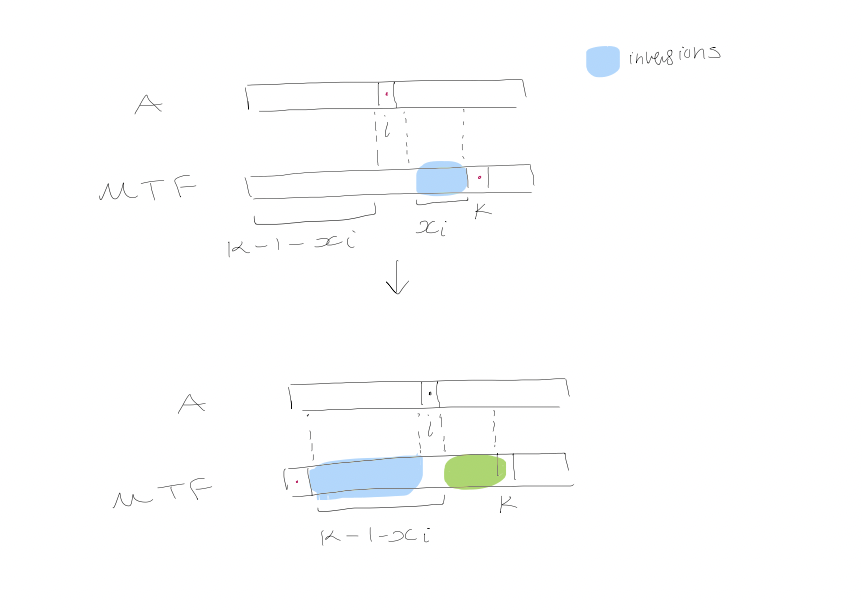
We run $A$ and $MTF$ in parallel, on the same request sequence $S$. The potential function $\phi$ is defined as the number of inversions* between $MTF$'s list and $A$'s list. Now, we bound the time of $access$.

Consider access by $A$ to position $i$ and assume we go to position $k$ is $MTF$'s list. Let $x_{i}$ be the number of items preceding the element in $MTF$'s list but not $A$'s list. So, the number of items preceding it in both lists is $k-1 - x_{i}$.

Moving the element to front in $MTF$'s list creates $k - 1 - x_{i}$ (between the element and those that used to precede it), and destroys $x_{i}$ inversions.

Amortized analysis: $$k + (k-1-x_{i}) - x_{i} = 2(k-x_{i}) - 1$$ Since $k-1-x_{i} \leq i-1$, we can conclude that $k-x_{i} \leq i$.

This gives us an amortized time of $\leq 2i - 1 = 2C_{A} - 1$ where $C_{A}$ is the cost of access for $A$ without exchanges (similar to insert/delete). An exchange by $A$ has $0$ cost to $MTF$, so the amortized time of an exchange by $A$ is increased in the number of inversions caused by exchange: $1$ for paid, $-1$ for free.

#skipped for now ... So, the total amortized cost is $$2C_{A}(S) - M + X_{A}(S) - F_{A}(S)$$

Conclusion

MTF is $2$-competitive

$$\begin{aligned} T_{A}(S) &= C_{A}(S) + X_{A}(S) \ T_{MTF}(S) &= C_{MTF}(S) \ &\leq 2C_{A}(S) + X_{A}(S) - F_{A}(S) - M \ &\leq 2T_{A}(S) \end{aligned}$$ * An inversion is defined as any pair of elements that appear in different orders relative to each other in different lists.

Pasted image 20250302145329.png

course-notes